Atlas de biodiversité : comment repérer des zones sous-prospectées ?
La réalisation d’un bon atlas faunistique (oiseaux, papillons, reptiles…) nécessite une bonne « pression de prospection ». Comment définir cette « pression de prospection » (ou « pression d’observation ») et comment détecter des secteurs sous-prospectés ?
Qu’est-ce que la « pression de prospection » et comment la mesurer ?
Un atlas faunistique est avant tout un ensemble de cartes de répartition d’espèce sur un territoire donné. Par exemple : l’atlas des oiseaux nicheurs de Bretagne, l’atlas des reptiles de Loire-Atlantique, etc. Pour réaliser ces cartes, on découpe le territoire en carrés, appelés « mailles ». Ces mailles font le plus souvent 10 km par 10 km. Quand une espèce est observée sur un site, on rapporte cette observation à la maille concernée. La présence d’une espèce sur une maille ne prête guère à discussion dès lors que l’identification de l’espèce est certaine. La question centrale dont dépend la qualité d’un atlas est : notre pression de prospection est-elle suffisante pour pouvoir affirmer que les mailles vides correspondent bien à des absences et non à des défauts de prospection. Autrement dit : alors que la présence d’une espèce sur un territoire n’a qu’une seule signification possible, l’absence est toujours sujette à caution.
La pression de prospection correspond aux efforts réalisés pour s’assurer de la présence ou de l’absence d’une espèce sur un territoire donné. Ces efforts peuvent être :
- d’ordre quantitatif : nombre de journées de prospection, nombre d’observateurs, surface prospectée, etc.
- d’ordre qualitatif : compétence / expérience des observateurs, diversité des milieux prospectés, techniques employées (pièges-photo, analyse de pelotes de réjection, détection acoustique des chiroptères, etc.)
On comprend dès lors qu’il est bien difficile de quantifier cette pression de prospection : un naturaliste expérimenté prospectant pendant une heure par semaine sera-t-il plus efficace qu’un observateur moins aguerris mais plus souvent sur le terrain ? Deux observateurs sont-ils deux fois plus efficaces qu’un seul ?
C’est pourquoi les auteurs d’un atlas essayent généralement de définir la pression de prospection a posteriori, en analysant les données et en croisant, par exemple, le nombre d’observations avec le nombre d’espèces découvertes.
Nombre d’espèce en fonction du nombre de données : une approche classique mais limitée
Une méthode d’analyse classique consiste à établir la relation entre le nombre de données par maille et le nombre d’espèces découvertes. On obtient quasiment toujours une courbe (car le nombre d’espèces est limité) de type : Nombre d’espèces = A*ln(nombre de données) – B (exemple ci-dessous)
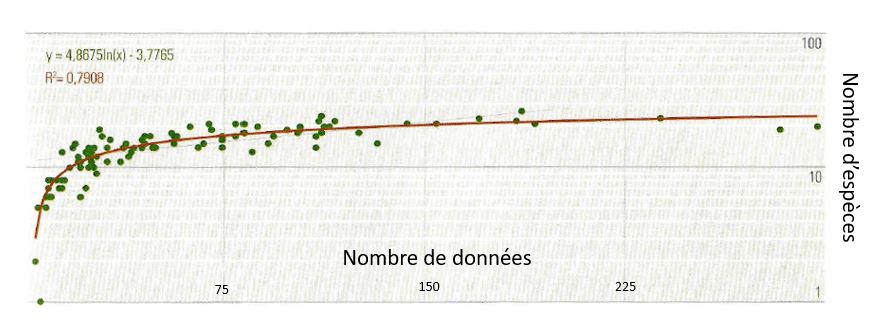
On repère ensuite le point d’inflexion et on note : « Au-delà de x observations, le nombre de données nécessaire pour détecter une nouvelle espèce augmente rapidement« . Ce que l’on peut encore traduire ainsi : « Une maille qui compte plus de x observations peut être considérée comme suffisamment prospectée« . En-dessous de ce seuil se trouveraient alors les zones sous-prospectées…
Cette méthode comporte de sérieux inconvénients. Tout d’abord, il n’y pas vraiment de relation mathématique entre le nombre de données et le nombre d’espèces, où alors avec une corrélation faible. Vous pouvez par exemple observer chaque jour dans votre jardin le même Rougegorge et ainsi augmenter de 365 le nombre de données sans améliorer sensiblement la qualité de prospection sur votre maille.
Mais surtout, le seuil retenu dans cette méthode est arbitraire : rien ne permet d’affirmer que la prospection est insuffisante en-dessous d’un certain nombre de données et suffisante au-dessus de ce seuil.
Une nouvelle méthode proposée par B.E.T
Nous avons donc mis au point une méthode qui s’affranchit du nombre de données et du nombre d’espèces par maille. Pour cela, nous nous sommes inspirés de la « théorie de l’information » de Shannon, à savoir la mesure de la quantité d’information contenue dans un ensemble de donnée. Dans notre, cas, cet ensemble de données est le tableau de présence / absence croisant les mailles et les espèces. Pour Shannon, l’information est la mesure de l’incertitude calculée à partir de la probabilité d’un évènement. Plus la probabilité qu’un évènement se produise est faible, plus sa réalisation nous offre d’information.
Dans le cas d’un atlas de biodiversité, certaines espèces sont très répandues et d’autres très rares. Si nous prenons l’exemple des reptiles :
- la présence du Lézard des murailles sur une maille nous apporte peu d’information car cette espèce est très commune et on s’attend à la trouver partout
- la présence de la Coronelle lisse sur une maille nous apporte davantage d’information car cette espèce est plus rare
Et réciproquement :
- l’absence du Lézard des murailles sur une maille nous donne beaucoup d’information
- l’absence de la Coronelle lisse sur une maille nous donne moins d’information
La méthode mise au point par B.E.T en 2020 est basée sur ce fait incontestable et bien connu des naturalistes : certaines espèces sont plus rares que d’autres. L’absence d’une espèce très commune n’a pas la même signification que l’absence d’une espèce rare.

Comment fonctionne concrètement la méthode P.A.C ?
Nous avons baptisé notre méthode P.A.C : Probabilité d’Absences Cumulées. Elle consiste à calculer la probabilité que plusieurs espèces soient simultanément absentes d’une même maille. P (absence cumulées) = P (absence espèce 1) x P (absence espèce 2) x … x P (absence espèce n).
Cette probabilité est comparée à la probabilité unitaire : P unitaire = 1 / nombre de mailles. Cela nous permet de voir si la combinaison des espèces absentes est statistiquement possible (= si elle peut se réaliser sur au moins une maille) ou si elle est statistiquement impossible.
Le résultat s’interprète de la manière suivante :
- si P (absences cumulées) / P unitaire > 1 cela signifie que la situation est statistiquement possible et donc que la prospection est satisfaisante
- si P (absences cumulées) / P unitaire < 1 cela signifie que la situation est statistiquement impossible et donc qu‘il y a un défaut de prospection
Le plus l’indice P.A.C est faible, le plus la sous-prospection est forte :
- indice PAC compris entre 1 et 0,1 = sous-prospection de niveau 1 (= légère)
- indice PAC compris entre 0,1 et 0,01 = sous-prospection de niveau 2 (= moyenne)
- indice PAC compris entre 0,01 et 0,001 = sous-prospection de niveau 3 (= forte)
- etc.
Mise en pratique
Pour montrer comment fonctionne notre indice, prenons l’exemple d’un atlas des reptiles sur un territoire fictif comportant 100 mailles. Dix espèces de reptiles ont été recensées, avec les fréquences suivantes :
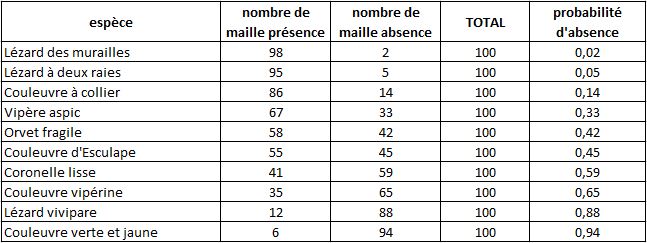
On voit que la probabilité que les Lézard des murailles soit absent d’une maille est faible. Cela arrive sur 2 mailles uniquement. A l’opposé, la probabilité d’absence de la Couleuvre verte et jaune est élevée. Une absence de cette espèce nous renseigne peu sur une éventuelle sous-prospection.
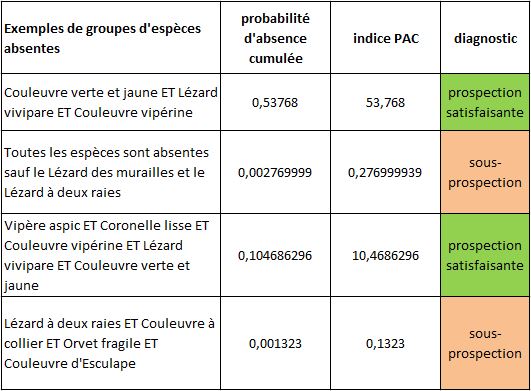
Considérons maintenant (tableau ci-dessous) le trio « Couleuvre verte et jaune / Lézard vivipare / Couleuvre vipérine ». La probabilité que ces trois espèces soient absentes simultanément d’une même maille vaut 0,94*0,88*0,65 = 0,53768. Cette absence cumulée doit donc statistiquement se produire sur 54 des 100 mailles de notre atlas. L’absence cumulée de ces 3 espèces n’a donc rien d’improbable, bien au contraire. Il n’y a donc aucune raison de suspecter une sous-prospection si ces 3 espèces sont absentes et toutes les autres présentes.
Prenons maintenant le quatuor « Lézard à deux raies / Couleuvre à collier / Orvet fragile / Couleuvre d’Esculape ». La probabilité d’absence cumulée est de 0,001323. Cette absence cumulée doit donc statistiquement se produire sur 0,1323 mailles… c’est à dire jamais. Elle indique donc une anomalie sur les mailles où elle se produit. Cette anomalie peut être interprétée comme une sous-prospection.
Une sous-prospection… ou autre chose ?
Nous venons de voir que certaines absences cumulées constituent une anomalie statistique. La cause la plus évidente de cette anomalie est la sous-prospection. Si l’on vous présente une maille sur laquelle toutes les espèces sont absentes, votre premier réflexe est de vous demander si elle a vraiment été prospectée !
Toutefois, il ne faut pas exclure la possibilité qu’une maille présente des conditions écologiques suffisamment originales pour exclure beaucoup d’espèces, et notamment des espèces très communes. Par exemple, à l’échelle nationale : les reptiles les plus communs de France (Lézard à deux raies, Lézard des murailles, Orvet fragile) sont absents de Corse. Mais cela ne signifie pas que la Corse soit mal prospectée. Attention donc aux interprétations trop hâtives, surtout sur un atlas à l’échelle nationale.
Enfin l’expérience montre que les mailles situées en périphérie de la zone d’étude ressortent souvent comme « sous-prospectées ». Mais cela n’a pas vraiment de sens dans la mesure où ces mailles périphériques, coupées par le trait de côte ou par une frontière administrative, ne sont que des demi-mailles, des quarts de mailles voire des dixièmes de mailles. Dans ce cas, à quoi bon se poser la question de la sous-prospection ? Une maille qui ne couvre que 10 km² de terrain ne peut pas être comparée à une maille « complète » couvrant 100 km².
Conclusion
La méthode des Probabilités d’Absences Cumulées (P.A.C) permet d’établir un seuil objectif en-dessous duquel une maille peut être considérée comme sous-prospectée. Plus l’indice P.A.C est faible, moins la prospection est satisfaisante. En-dessous de 1, on peut considérer qu’il y a sous-prospection sauf si une cause purement biogéographique (comme l’insularité) permet d’expliquer l’anomalie statistique. Notre méthode est donc un outil utile et a priori efficace mais qui ne dispense pas de réfléchir.







Bonjour, je m’intéresse à l’évaluation de la pression de prospection dans le cadre d’inventaires entomologiques.
J’ai lu votre article et je trouve votre indice de probabilités d’absences cumulées très intéressant. Cependant, il me semble avoir remarqué une anomalie dans le calcul. En effet, dans le cas où une espèce serait présente sur la totalité des mailles, sa probabilité d’absence serait égale à 0. Le problème étant qu’en calculant la probabilité d’absence cumulée, il faut faire un produit de toutes les probabilités d’absence mais ce résultats donnera inévitablement un 0 si une des espèces a une probabilité d’absence égale à 0.
Est-ce normal? Pouvons-nous tirer des conclusions correctes d’un tel résultat?
Je vous remercie d’avance pour votre réponse.
Bonne journée à vous.
Bastien Fiaschi
Bonjour,
Content que cet indice vous intéresse. En effet, si une espèce est présente sur 100 % des mailles, cela pose le problème que vous évoquez (multiplication par 0). Dans les faits, je n’ai jamais trouvé d’exemple d’espèce présente sur 100 % des mailles d’un atlas. Même pour les espèces les plus communes (par exemple le Vulcain chez les papillons ou le Lézard des murailles chez les reptiles), il y a toujours quelques « blancs », souvent liés à un défaut de prospection.
Si jamais vous avez le cas d’une espèce présente à 100 %, l’espèce en question peut être retirée du calcul : n’étant absente nulle part, elle ne donne aucune information sur une éventuelle sous-prospection. Pour dire les choses autrement, puisque nous raisonnons sur des absences, nous n’avons pas de raison de considérer les espèces qui n’ont pas d’absence.
Par curiosité, pourriez-vous me dire quelle espèce est présente sur 100 % des mailles ?
Bien cordialement
Émilien Barussaud
Bonjour,
Merci beaucoup pour votre réponse et pour ces clarifications. Je saisie mieux la logique sur laquelle est calculée l’indice.
En réalité, je ne suis encore jamais tombé sur une telle situation mais j’en ai seulement envisagé la possibilité avec des espèces très communes comme le Vulcain en effet. Il est vrai qu’à l’échelle d’un atlas, cette situation est tout de même peu probable. Je saurai quoi faire si cela arrive en tout cas!
Merci encore et bonne journée.
Bastien Fiaschi